For two days now we have discussed answers to the question

You drink a glass of ordinary tap water. How many water molecules in this glass were in the blood of Socrates when he died?

First we used probability to determine that the value is at least tens of thousands of molecules. Then we realised that water is actually not a stable molecule, which reduced the value to zero. Of course we could revert back to the original solution by choosing to look at something that is stable – say argon in the last breath of Socrates, as Grimvall suggests.

More similar than that.
(Diane Arbus – Identical twins, Roselle, N.J. 1966, 1966)

But that, unfortunately, will not save us either. The real answer is that it’s a question we are not allowed to ask! Not in a “freedom of speech” sense, but rather that from a physical point of view, the question, and any answer to it, makes no sense.

Why?

Because particles are identical. Really identical! One electron is just like any other electron. And one molecule of water is just like any other molecule of water. This means that we cannot, even in principle, label a specific molecule – there are no Jane and John Water. As soon as our Jane and John would bump each other their wave functions will overlap, and they will both be both Jane and John. And when they separate each will be a mixture of JaneJohn. We could theoretically imagine that we could try to follow a single molecule – all the time keeping our eyes on it – and never mixing it up with any other. This actually happens in Penning traps, where a single ion can be trapped for months at a time in extremely good vacuum¹. In a liquid, the molecules constantly bounce around and the time between collisions is measured in picoseconds rather than months or years.

Grimvall uses an analogy of money: it makes perfect sense to wonder about what the chance is of a particular 10€ banknote you used for paying your beer coming back to you after circulating through the monetary system, while asking the same questions when using your credit card makes no sense at all. As an analogy it is helpful, up to a point, but electronic money is just a notation, whereas atoms and molecules are physical things, like the banknote that still are indistinguishable. The (inconvenient) truth, as with so much that concerns quantum physics, is that there are no objects in our macroscopic world that function in this way. Two new, shiny coins might look extremely similar, but only until you look close enough. On a microscopic level they are quite different! Because of our lack of experience with truly indistinguishable objects, our intuition leads us astray. This happens all the time when dealing with quantum system, which is a reason² for quantum mechanics to be described as strange™.

The setup for Gibbs paradox.

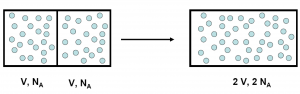
We shouldn’t feel too bad about our failure to see this trap.³ Josiah Willard Gibbs, one of the giants of theoretical physics and founders of physical chemistry, was thinking hard about a problem which has become known as Gibbs paradox. The problem setup, somewhat artificial, is that if we have a box with two equal compartments, each filled with the same number of atoms of an ideal gas. If we remove the barrier between the compartments, and let the gas mix, we haven’t really changed anything. If we insert the barrier again, we are back where we started. But calculating the change in entropy (a measure of the number of states that the system can be in) when we remove the barrier using the classical notion of particles we see that the entropy has increased. This is because the gas in each compartment suddenly have more space, and thus more states, available to fill. And if insert the barrier again, it decreases. This seems to break the second law of thermodynamics, which states that the entropy of a closed system⁴  always increases. This is not good, because physicists really like the laws of thermodynamics. The solution is to realise that when we mix identical particles we are actually not doing anything at all. If we exchange places between two of the particles, the system itself remains completely unchanged. But it took a Gibbs to realise this.

So there we have it. A deceptively simple question, with a surprising answer. But a question where even the wrong answers teach us something.

1. About 10^-13 Pa or better
2. Regardless of the objective fact that it is bloody strange!
3. In fact most text-book authors seem to miss it too. As a student often argued, mostly futilely, with people about that problem and was very pleased when I saw that Grimvall took this up in his book on brainteasers.
4. We have to assume that the barrier is infinitely thin, light and can be moved without using any energy – or at least an arbitrarily small amount of energy.